SHADER에서 사각형 그리기

1. 기본 함수

Iñigo Quilez – fractals, computer graphics, mathematics, demoscene and more의 Box – signed를 민수님의 방법을 사용해서 2차원 함수로 변환하여 분석해보려고 한다.

float sdBox( vec3 p, vec3 b )
{
  vec3 d = abs(p) - b;
  return min(max(d.x,max(d.y,d.z)),0.0) +
         length(max(d,0.0));
}

2차원 함수로 변환했다.

float sdBox2(vec2 p, vec2 b){
    vec2 d = abs(p) - b;
    return min(max(d.x, d.y), 0.0) + length(max(d, 0.0));
}

2. 순서

이 함수는 다음과 같은 구조를 하고 있다.

1) d를 position으로부터 생성한다.

vec2 d = abs(p) - b;

2) d로부터 계산

min(max(d.x, d.y), 0.0)

3) d로부터 계산

length(max(d, 0.0))

4) 2와 3을 더해 리턴한다. 따라서 이 순서로 진행해보겠다.

3. position 나타내기

일단 기본이 되는 그래프부터 표현해보도록 한다. GLSL Sandbox에서 다음과 같은 코드로 시작한다.

#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 resolution;

void main( void ) {
    vec2 p = gl_FragCoord.xy / resolution.xy;
    p = p * 2.0 - 1.0;
    float color = position.x;
    gl_FragColor = vec4( color, color, color, 1.0 );
}

다음과 같은 결과를 확인할 수 있다.

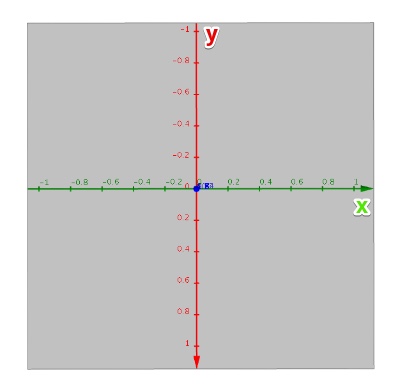
현재 color값에 p.x의 값이 들어간 것을 확인할 수 있다. 즉 좌측 상단부터 (0, 0) 우측 하단까지 (1, 1)의 값을 가지는 것을 알 수 있다. 이는 다음과 같은 그래프로 표현할수 있다.

x, y가 갖는 값을 z축에 대입하여 3d그래프로 표현해보았다.

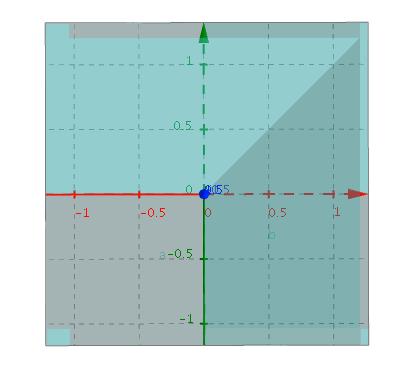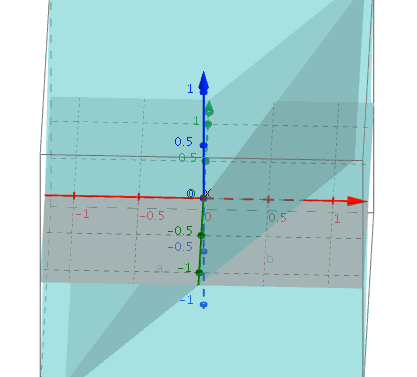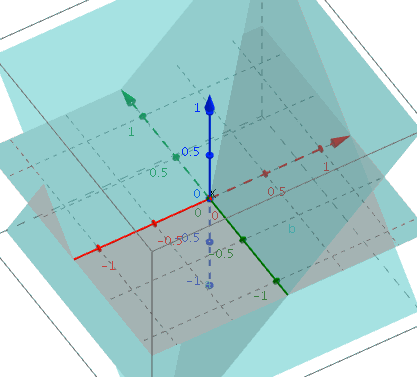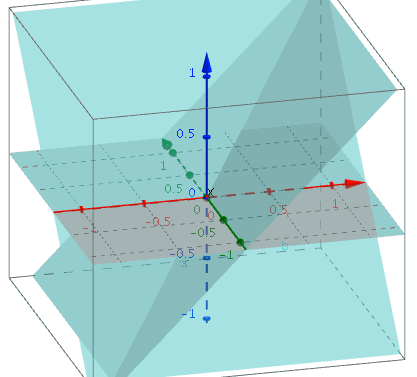
4. `vec2 d = abs(p) - b;` 보기

위의 position값에서 abs(p) 는 절대값이기 때문에 다음과 같이 표현할 수 있다.

b는 vec2값이기 때문에 x, y에 둘다 동일한 값을 빼준다고 가정하면 vec2 d = abs(p) - b;는 다음과 같이 표현할수 있다.

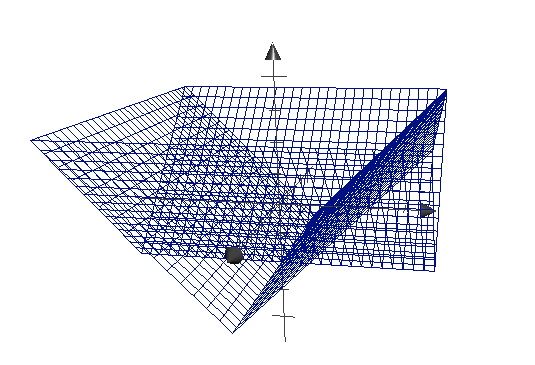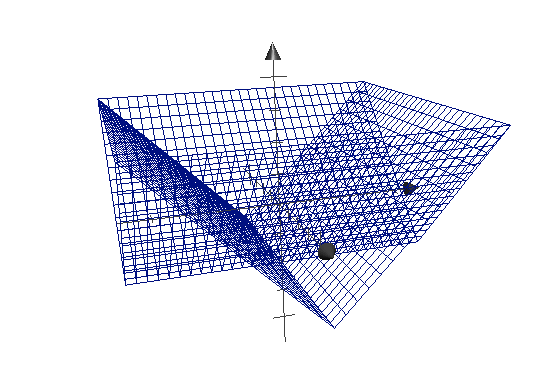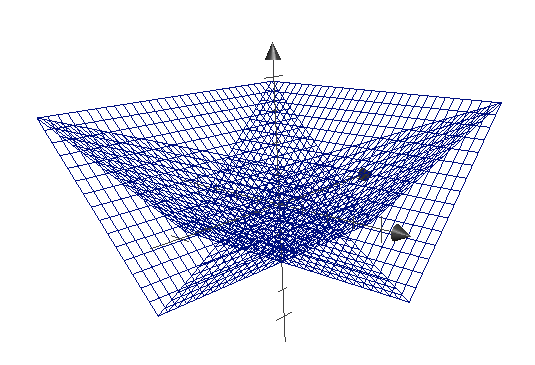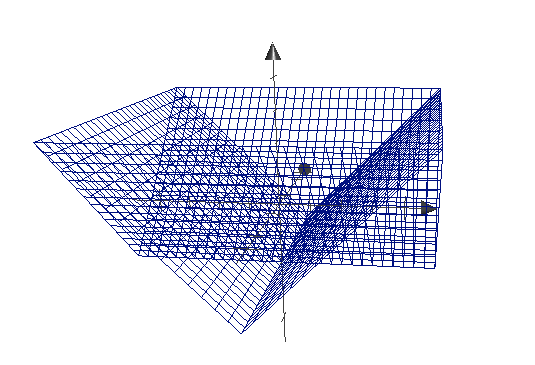
color = d.x를 glslsandbox에서 아래와 같은 코드로 실행했다.

#ifdef GL_ES
precision mediump float;
#endif

uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;

void main( void ) {
    vec2 pos = ( 2.0 * gl_FragCoord.xy - resolution.xy ) / resolution.x;
    float color;
    vec2 d = abs(pos) - 0.5;
    color = d.x;    
    gl_FragColor = vec4( vec3(color), 1.0 );
}

그래프를 보면 가운데에 0보다 작은 영역이 어둡게 표현되었음을 알 수 있다.

5. `min(max(d.x, d.y), 0.0)`

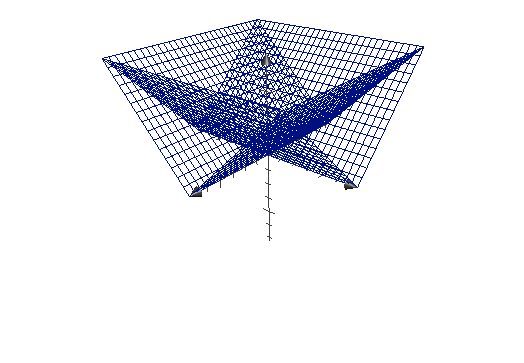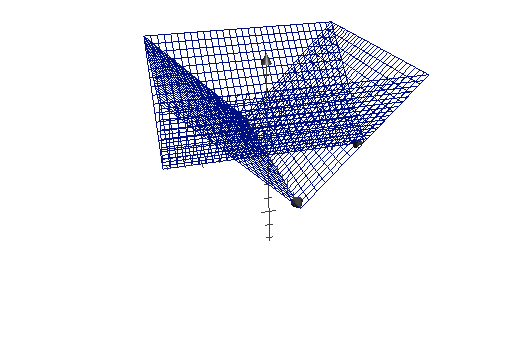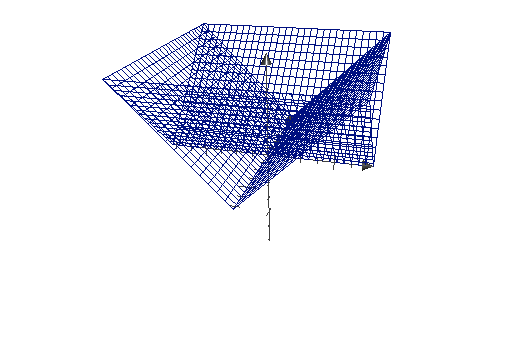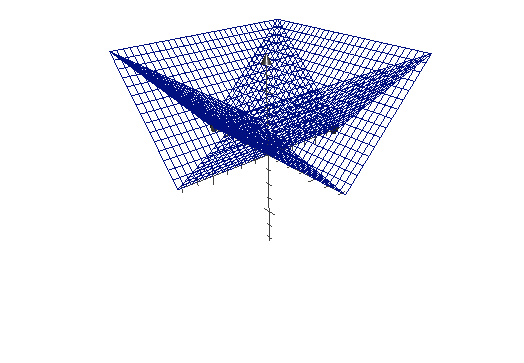
3에서 d.x를 shader에서 표현해보았는데, 이번에는 max(d.x, d.y)를 그래프에 먼저 표현해 보겠다.

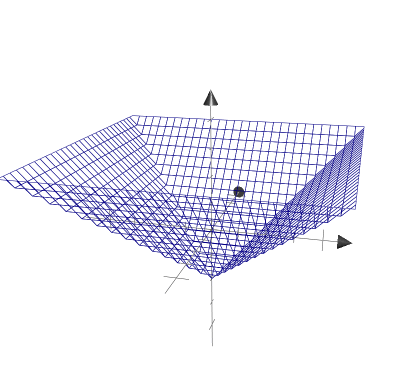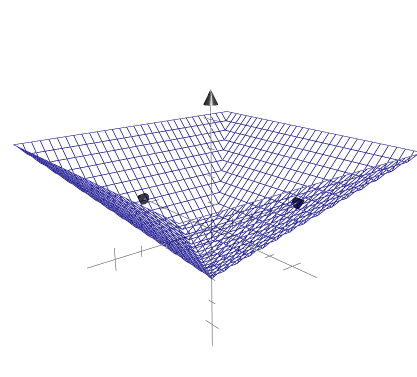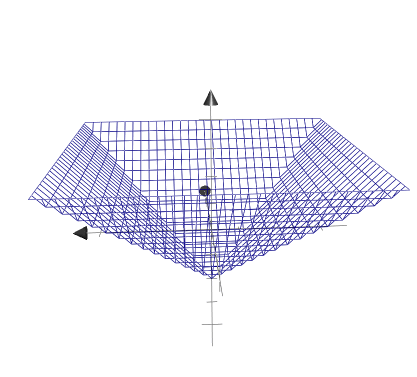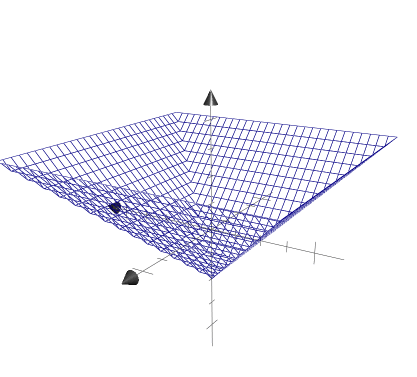
이전까지는 x에 관한 부분과 y에 관한 부분이 각각 따로 떨어져 있어 color에 대입하려고 해도 d.x나 d.y처럼 각각 따로 할 수 밖에 없었는데, max함수로 마치 두개의 식을 한 식에 표현한 듯한 모양을 얻을수 있다. 또한 이 그래프에서 z축의 단면과 만나는 부분이 사각형을 이루는데 이 부분을 shader에서 표현해 보겠다.

    vec2 d = abs(pos) - 0.5;
    color = max(d.x, d.y);

그래프에 나타난 대로 0보다 작은 수는 어둡게 표현되었다.

min(max(d.x, d.y), 0.0)

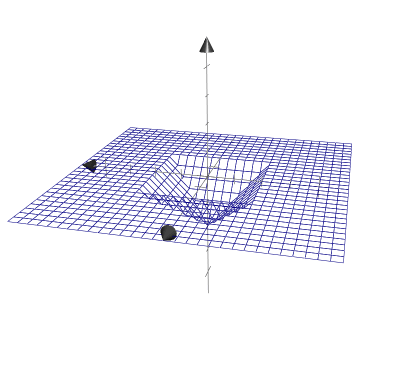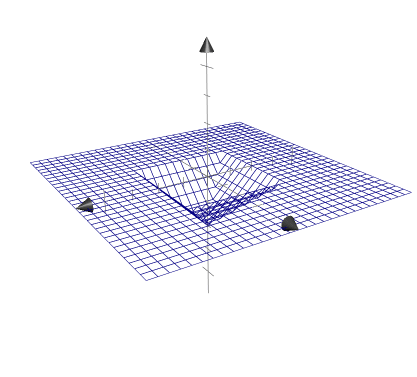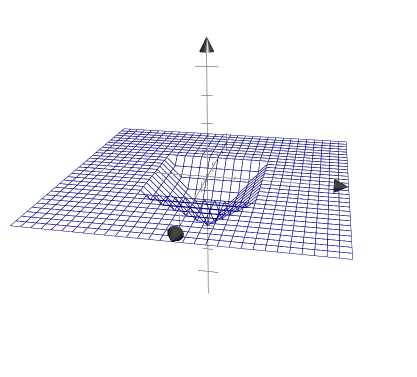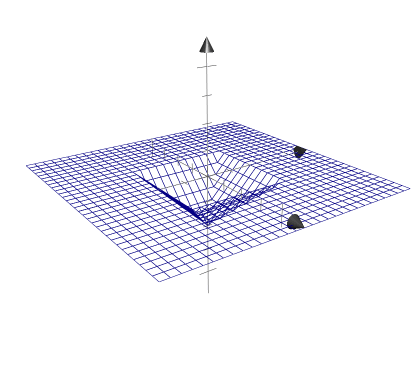
0보다 작은수만 남았기 때문에 0보다 큰수는 지워졌다. 실제로 이 코드를 shader해보면 까만 화면밖에 나오지 않는다. 남은 부분을 볼수 있게 하기 위해 마지막에 -1을 곱해주었다.

    color = min(max(d.x, d.y), 0.0);
    color = -1.0 * color;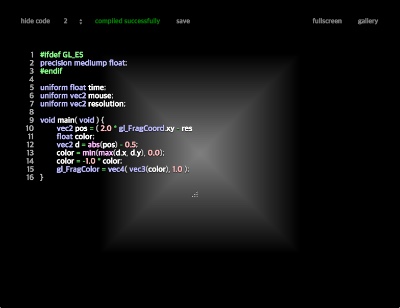

smoothstep를 적용해 주었다.

color = smoothstep(0.3, 0.31, color);

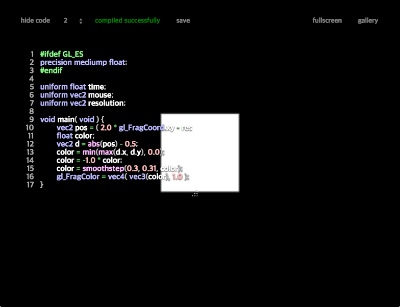
위의 과정을 거쳐 사각형 모양을 얻을 수 있다.

KMYH

code, visual & scrupture